寻找颗粒混合体的最大相对密度 (binary mixture)
这个问题挺古老的,但只有最近几十年随计算机的发展,才有可能真正进行模拟。二维的模拟比较简单,也很直观,可惜这个世界更多是三维的。三维的问题就多了,计算成本、边界效应、结果的可视化...
最先知道这个问题,是在大学的时候看分形几何(Fractal Geometry)的书。大概的故事是,如果考虑到混凝土的搅拌,如何才能得到最高的相对密度,以增强材料的强度?几个搞分形几何的科学家说找到一种配比,“号称”可以用混凝土建更高的大楼,而不采用钢结构。
这个倒不是真正的研究目的,做这个问题的原因是要寻找一个给离散单元法(DEM)计算的初始构型。要求颗粒之间没有预应力,并能够达到比较高的相对密度。找到了一个随机球装问题的算法,于是开始了计算。发现影响最终结果的因素也太多了一点,最简单的问题是相同尺寸的颗粒。如果考虑不同尺寸,就有太多的随机分布可以选择。就算是简化以后,一个系统只有两种不同尺寸的颗粒(binary mixture)。参数包括:两种颗粒尺寸的比值,两种颗粒所占的相对体积。
其实,在现实中,这种混合经常采用振动的方法,而对于尺寸相差过大的颗粒混合体,很容易就产生颗粒的分离,例如大的在上、小的颗粒在下层,即所谓“巴西果效应”(Brazil nut effect)。
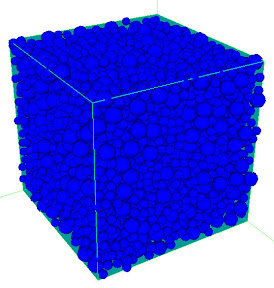
对于比较大规模的系统,消耗的CPU时间已经是无法忍受了。改进算法以后,今天算是得到些初步的结果,最后的结果应该是有趣的,可惜需要基于大量的计算数据。下图所示为一个试算的可视化,采用OpenGL做的后处理。
N5000 Binary System R1=0.04420836, R2=0.02652502, RD=0.5. Packing Factor: 64.31%.