变化
没有下一代的时候,搬个家换个工作什么的都是可以将就的。两个人住10平米的房子也还是可以忍受的,甚至还有那么点乐趣。在一个吵闹的街区,就晚上关窗睡觉;在一个治安不好的地方,就夜里尽量不出门;离单位近就走路去上班,离单位远就在公交车上或者睡觉或者看书……这就是之前几年在德国生活的心态。
有了下一代,就开始考虑各种各样的问题了。例如,工资够不够养家,房子面积大不大,附近治安和社区环境如何,有没有供孩子玩耍的公园,有没有好的幼儿园,有没有好的小学中学大学(虽然现在孩子都还不会爬)……
已经到了一个应该做点选择的时候了,其实窝在这个德国乡下也是一种选择,只要耐得住寂寞。最近,帮附近几家中国人搬家,都是从原来租的公寓里面搬出来,搬到新造好的别墅里。在休息的时候,蹲在他们家的门槛上想了想:可能这就是我呆在这里十几年以后的状况。固然有点田园色彩。不远万里到欧洲当个“农民”、住在“乡下”也不是一件坏事。在欧洲买别墅造房子的压力尚且比不过在国内一线城市买公寓的压力,买完以后土地和房子都是你自己的,没有听说过什么70年年限的说法。在这里搞事业,虽然也要依靠一点关系,但基本上是靠能力吃饭的;国内似乎是一个相反的状态。
但是,如果从现在可以一直望到十几年后的自己,一成不变的工作和生活的循环,没有太多的变化。似乎有一丝绝望,似乎有一丝不甘。更不用说下一代的教育问题了,等到他们成年,已经没有太多可以选择的可能了。
我之前和这里的中国同事聊天,说到想走,往往得到的第一个反应就是“难道合同不能延了?”我又不想去纠正说,其实是想要点变化,这样显得我在卖乖。找个新地方也不是那么容易的,就像上面说的那么多需要考虑的因素。美国的牛校暂时就不考虑了,因为学校牛,往往博士后的工资就相对低,而且工作不稳定,面临着经常换地方的可能。对于一个有家有口的中年男人来说,这是一种说不出的痛苦。
其实,选择也是很多的。查找资料的过程中,找到当年搞自助游的乐趣了。
PS:参考了一下悉尼的租房价格,看两室一厅的公寓,一看才五百澳元,正自喜的时候,发现后面的单位是每周 ……

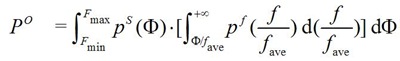
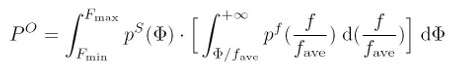

 从德国的一家不太大的网上书店购得 Immanuel C.Y. Hsü (徐中约)的 The Rise of Modern China (the 6th edtion, Oxford University Press)。作者是加州大学Santa Barbara分校的历史学教授,翻译成中文书名为《中国近代史》。
从德国的一家不太大的网上书店购得 Immanuel C.Y. Hsü (徐中约)的 The Rise of Modern China (the 6th edtion, Oxford University Press)。作者是加州大学Santa Barbara分校的历史学教授,翻译成中文书名为《中国近代史》。